Étude théorique d'une éolienne
Énergie fournie par le vent
Énergie cinétique
Le vent est de l’air en mouvement, et comme tout corps en mouvement on peut lui associer une énergie cinétique, elle est en fonction de la masse et de la vitesse du volume d'air. Si on considère que la masse volumique de l'air (masse de l'air par unité de volume) est constant, on peut dire que l'énergie fournie par le vent est fonction de sa vitesse :

 : masse du volume d'air (en kg)
: masse du volume d'air (en kg)
 : vitesse instantanée du vent (en m/s)
: vitesse instantanée du vent (en m/s)
 : énergie cinétique (en joules)
: énergie cinétique (en joules)
La masse de l’air
A une pression atmosphérique normale et à une température de 15 degrés Celsius, l'air possède une masse volumique d'environ 1,225 kg par mètre cube. Cependant, la masse volumique diminue un peu lorsque l'humidité de l'air augmente. De même, l'air froid est plus dense que l'air chaud, tout comme la masse volumique de l'air est plus faible à des altitudes élevées (dans les montagnes) à cause de la pression atmosphérique plus basse qui y règne.

 : masse du volume d'air (en kg)
: masse du volume d'air (en kg)
 : volume d'air occupé (en m3)
: volume d'air occupé (en m3)
 : masse volumique (en kg/m3)
: masse volumique (en kg/m3)
Dans le cas de l’éolien, le volume d'air occupé dépend de la surface balayée par le rotor de l’éolienne. La puissance du vent traversant le rotor correspond à la quantité d’énergie cinétique traversant le rotor à chaque seconde.
Énergie théoriquement récupérable
En considérant un dispositif de récupération de cette énergie de surface S et en faisant l'hypothèse que la vitesse du vent est identique en chaque point de cette surface, le volume d'air qui traverse cette surface en 1 seconde est égale à vS.

 : puissance récupérable (Watt)
: puissance récupérable (Watt)
 : débit massique du volume d'air traversant la surface S en 1 seconde (kg/s)
: débit massique du volume d'air traversant la surface S en 1 seconde (kg/s)
 : masse volumique de l'air (kg/m3)
: masse volumique de l'air (kg/m3)
 : vitesse de l'air traversant le dispositif (m/s)
: vitesse de l'air traversant le dispositif (m/s)
 : surface du dispositif de récupération (m2)
: surface du dispositif de récupération (m2)
 : débit volumique d'air (m3/s)
: débit volumique d'air (m3/s)
Ce qui revient à la formule qui suit.
Puissance récupérable


 :
:
 : vitesse du fluide au niveau de la turbine (en m/s)
: vitesse du fluide au niveau de la turbine (en m/s)
 : masse volumique de l'air (air atmosphérique sec, environ : 1,23 kg/m3 à 15 °C et à pression atmosphérique 1,0132 bar)
: masse volumique de l'air (air atmosphérique sec, environ : 1,23 kg/m3 à 15 °C et à pression atmosphérique 1,0132 bar)
 : surface projetée du capteur éolien (en m2)
: surface projetée du capteur éolien (en m2)
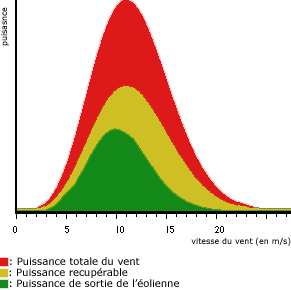
Cette puissance (en Watt) est une puissance théorique, il est bien sûr impossible qu'elle soit récupérée en totalité par une éolienne (cela reviendrait à arrêter le vent).
Les éoliennes détournent le vent
En pratique, une éolienne sert à récupérer l'énergie du vent, en contrepartie celle-ci dévie le vent avant qu'il atteigne la surface balayée par le rotor. Une éolienne ne pourra donc jamais récupérer l'énergie totale fournie par le vent (voir loi de Betz). Lorsque l'énergie cinétique du vent est convertie en énergie mécanique par le rotor, le vent est freiné par celui-ci, la vitesse du vent en amont du rotor est toujours supérieure à celle en aval. Or la masse d'air qui traverse la surface balayée par le rotor est identique à celle sortant (le débit massique est conservé). Il en résulte un élargissement de la veine d'air (tube de courant) à l'arrière du rotor. Ce freinage du vent est progressif, jusqu'à ce que la vitesse de l'air à l'arrière du rotor devienne à peu près constante.
Variation de la masse volumique de l'air
La masse volumique ( ) varie avec différents paramètres :
) varie avec différents paramètres :
- l'altitude (pression de l'air) : plus l'altitude est élevée et plus la masse volumique de l'air sera faible. Une même éolienne produira plus en bord de mer qu'en haute montagne avec la même vitesse de vent
- la température : plus la température est élevée et plus la masse volumique de l'air sera faible. Une éolienne produira plus lorsque la température ambiante sera faible
- l'humidité relative de l'air : plus l'air sera humide et plus la masse volumique sera faible mais l'influence de l'humidité relative de l'air sur la masse volumique reste relativement faible
Limite de Betz/Formule de Betz
La puissance récupérable est inférieure, puisque l'air doit conserver une énergie cinétique résiduelle pour qu'il subsiste un écoulement. L'allemand Albert Betz a démontré en 1919 que la puissance maximale récupérable est :

avec  ,lorsque
,lorsque 
 : masse volumique du fluide (air atmosphérique sec, environ : 1,23 kg/m3 à 15 °C et à pression atmosphérique 1,0132 bar)
: masse volumique du fluide (air atmosphérique sec, environ : 1,23 kg/m3 à 15 °C et à pression atmosphérique 1,0132 bar)
 : surface du capteur éolien (en m2)
: surface du capteur éolien (en m2)
 : vitesse incidente (amont) du fluide (en m/s)
: vitesse incidente (amont) du fluide (en m/s)
Le rendement maximal théorique d'une éolienne est ainsi fixé à  , soit environ 59,3 %. Ce chiffre ne prend pas en compte les pertes d'énergie occasionnées lors de la conversion de l'énergie mécanique du vent en énergie électrique.
, soit environ 59,3 %. Ce chiffre ne prend pas en compte les pertes d'énergie occasionnées lors de la conversion de l'énergie mécanique du vent en énergie électrique.
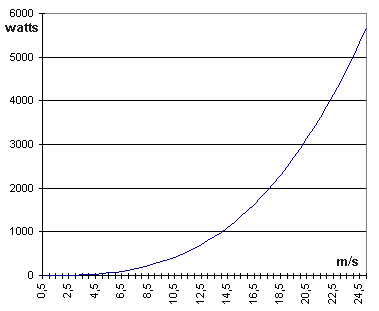
Dans le cas d'une hélice de diamètre D, la limite de Betz est égale à :


La puissance fournie par un aérogénérateur est proportionnelle :
- au carré des dimensions du rotor
- au cube de la vitesse du vent
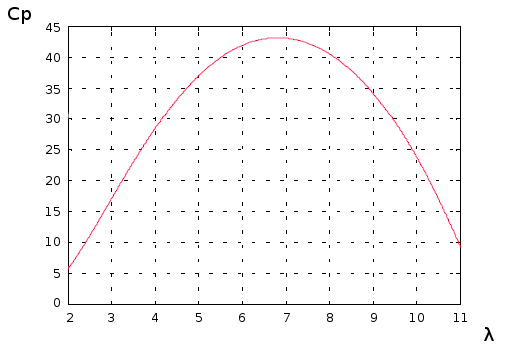
Courbe ci-contre pour une hélice de diamètre D = 1m.
Rendements
L'énergie fournie par l'aérogénérateur étant convertie d’une forme à une autre, cette limite est donc affectée par tous les rendements propres aux différentes transformations.
- Hélice :

- Le multiplicateur ou le réducteur :

- L'alternateur ou la génératrice continue :

- Le transformateur :

- Le redresseur :

- Les batteries :

- Les pertes de lignes :

Les rendements de chaque élément varient avec le régime de fonctionnement lié à la vitesse de rotation de l'hélice, ce qui en dehors du régime nominal diminue encore le rendement global du dispositif, il semble difficile de dépasser 70% de la limite de Betz.
Le potentiel éolien
Le potentiel éolien théorique mondial est de 106 TWh/an. La production mondiale (2011) s'élève à 460TWh/an. La consommation mondiale d'électricité (2011) est de 20 000 TWh/an.
La distribution de Weibull
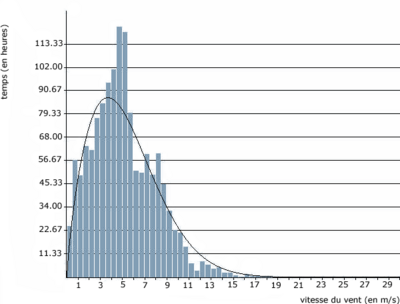
On décrit normalement les variations du vent sur un site donné en utilisant une distribution de Weibull comme celle que vous voyez sur l'image ci-contre. C'est le modèle général qui décrit les variations de la vitesse du vent. Ce modèle permet d'optimiser la conception des éoliennes pour minimiser les coûts liés à la production d'électricité.
Le coefficient de Weibull traduit la distribution des vitesses du vent et est déterminé par la courbe de distribution Weibull. Pour un facteur de forme égale 2 on parle de la distribution de Rayleigh.
Construction
On mesure la vitesse moyenne du vent toutes les 10 minutes au moyen d'un anémomètre. Les valeurs obtenues sont alors réparties en différentes vitesses de vent. On peut alors exprimer le potentiel énergétique d'un site en fonction de la fréquence des différentes classes de vitesse.
Fonction de probabilité de densité de Weibull
![Equation $$ f(v) = \left ( \frac{k}{c} \right ).\left ( \frac{v}{c} \right ) ^{(k-1)}.\exp \left [ -\left ( \frac{v}{c} \right ) \right ] ^k $$](/lib/exe/fetch.php?media=wiki:latex:/img30eac8dd47c7c1c97576d607de6c6459.png)

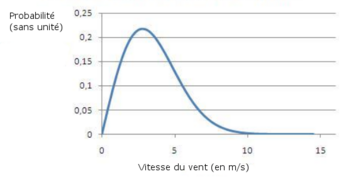
La fonction de densité de probabilité de Weibull est destinée à refléter la probabilité qu'un événement se produise entre deux points. L'aire sous la courbe entre deux vitesses de vent supérieures à zéro sera égale à la probabilité que le vent souffle quelque part entre ces deux vitesses. Sur la courbe de puissance ci-contre, nous pouvons déterminer les constantes des paramètres de Weibull :
 est le facteur de forme de Weibull. Il donne la forme de la distribution et prend une valeur comprise entre 1 et 3. Plus la valeur est faible et plus la vitesse du vent est variable tandis-qu'une valeur de k élevée indique une vitesse de vent constante.
est le facteur de forme de Weibull. Il donne la forme de la distribution et prend une valeur comprise entre 1 et 3. Plus la valeur est faible et plus la vitesse du vent est variable tandis-qu'une valeur de k élevée indique une vitesse de vent constante.
 est le facteur d'échelle de Weibull exprimé en m/s. Il permet d'exprimer la chronologie d'une vitesse caractéristique.
est le facteur d'échelle de Weibull exprimé en m/s. Il permet d'exprimer la chronologie d'une vitesse caractéristique.  est proportionnel à la vitesse moyenne du vent.
est proportionnel à la vitesse moyenne du vent.
Dans le cas de la courbe ci-contre :
- paramètre de forme : k = 1,751311
- paramètre d'échelle : c = 5,986052.
L'aire sous la courbe est définie par :

Dans l'exemple ci-contre, la probabilité pour que le vent souffle entre 3 m/s et 4 m/s est de : F(4) – F(3) = 0,38958 – 0,25788 soit 13,17%
La distribution de Rayleigh
La distribution de Rayleigh est un cas particulier de la distribution de Weibull pour le cas où le facteur de forme k est égal à 2. Les fabricants fournissent souvent les calculs de performance en utilisant la distribution de Rayleigh.
![Equation $$ f(v) = 2. \left ( \frac{v}{c^2} \right ).\exp \left [ -\left ( \frac{v}{c} \right ) \right ] ^2 $$](/lib/exe/fetch.php?media=wiki:latex:/img16741f945f74c9531b0e0c616dc5071d.png)
La puissance moyenne
La puissance moyenne du vent est déterminée grâce à la distribution de Weibull, connaître la vitesse moyenne du vent ne suffit pas à calculer la puissance moyenne. Il faudra prendre en compte la probabilité de l'occurrence de chaque vitesse de vent et la puissance correspondante, car la puissance est proportionnelle au cube de la vitesse. Les vents forts contenant le plus d'énergie influeront d'autant plus sur la puissance moyenne, bien qu'ils aient une faible probabilité.
La puissance du vent
En multipliant la puissance de chaque vitesse de vent par la probabilité de l'occurrence de cette vitesse selon la répartition de Weibull, nous pouvons calculer la distribution de l'énergie éolienne (en kWh/m²/an ou en W/m²) à des vitesses de vent différentes, cette distribution est appelée la densité de puissance.
Variation de vitesse du vent en fonction de la hauteur
Action du vent sur les pales
Vitesse angulaire du rotor
La vitesse angulaire  , aussi appelée fréquence angulaire ou pulsation, est une mesure de la vitesse de rotation. C'est-à-dire un angle par seconde
, aussi appelée fréquence angulaire ou pulsation, est une mesure de la vitesse de rotation. C'est-à-dire un angle par seconde

 : vitesse angulaire (en rad/s)
: vitesse angulaire (en rad/s)
 : fréquence de rotation du rotor (en s-1 ou Hz)
: fréquence de rotation du rotor (en s-1 ou Hz)
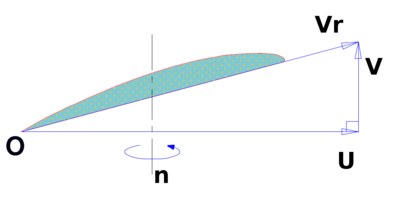
Vitesse tangentielle
Soit une hélice immobile dont l'axe de rotation est parallèle au vent, pour chaque pale on peut tracer la résultante perpendiculaire au profil appliquée au centre de la poussée aérodynamique.
On obtient:
 et
et  parallèles et de même sens qui ont tendance à déplacer l'hélice dans un mouvement de translation dans la direction du vent
parallèles et de même sens qui ont tendance à déplacer l'hélice dans un mouvement de translation dans la direction du vent et
et  parallèle et de sens opposé, perpendiculaire à la direction du vent
parallèle et de sens opposé, perpendiculaire à la direction du vent
Ces deux forces créent un couple moteur qui a tendance à faire tourner l'hélice dans un plan perpendiculaire à la direction du vent.

 : vitesse du vent dû au déplacement de la pale ou vitesse tangentielle (en m/s)
: vitesse du vent dû au déplacement de la pale ou vitesse tangentielle (en m/s)
 : vitesse angulaire du rotor (en rad/s)
: vitesse angulaire du rotor (en rad/s)
 : distance du point considéré à l'axe de rotation (en m)
: distance du point considéré à l'axe de rotation (en m)
 : fréquence de rotation du rotor (en hertz == s-1 == tour/seconde)
: fréquence de rotation du rotor (en hertz == s-1 == tour/seconde)
 : fréquence de rotation du rotor (en (tour.K+1)/(seconde.K-0)
: fréquence de rotation du rotor (en (tour.K+1)/(seconde.K-0)
 : fréquence de rotation du rotor (en (tour.K+0)/(seconde.K-1)
: fréquence de rotation du rotor (en (tour.K+0)/(seconde.K-1)
avec K+1 élément de R*+ , donc K+1 > 0
 : fréquence de rotation du rotor (en tour/min)
: fréquence de rotation du rotor (en tour/min)
Vitesse relative
Le vent vu par la pale est en fait une composition du vent réel et du vent créé par le déplacement de la pale (qui varie sur toute la longueur de la pale proportionnellement au rayon), ce vent résultant est appelé vent apparent ou vent relatif, la vitesse de ce vent résultant par rapport à la pale est supérieure à la vitesse propre de la pale.
D’après le théorème de Pythagore, la vitesse relative au carré est donnée par la somme des carrés de la vitesse du vent et la vitesse tangentielle de la pale.

 : vitesse relative de la pale (en m/s)
: vitesse relative de la pale (en m/s)
 : vitesse du vent (en m/s)
: vitesse du vent (en m/s)
 : vitesse tangentielle du point considéré (en m/s)
: vitesse tangentielle du point considéré (en m/s)
Induction
La vitesse et l'angle réellement perçue par le profil de la pale encore modifié par l'induction de l'hélice. Ce phénomène modifie la trajectoire du fluide en amont de la pale. L'induction comporte une composante axiale et une composante tangentielle. Pour comprendre le phénomène d'induction on peut par exemple prendre une hélice d'avion. Même si l'avion ne se déplace pas, lorsque son hélice tourne, avant le décollage, il est très dangereux de se placer devant l'hélice car elle "aspire" de l'air en amont: c'est l'induction axiale. Pour une éolienne cette induction "freine le fluide" légèrement en amont. Ne pas tenir compte des phénomènes d'induction entraînes des angles et des vrillages erroné. Le calcul de l'induction se fait grâce a la théorie des élément de pales (valable pour tous les type d'hélices propulsives ou caprices). L'utilisation de logiciel de conception d’hélice éolienne 1) est nécessaire pour résoudre les vitesses induites.
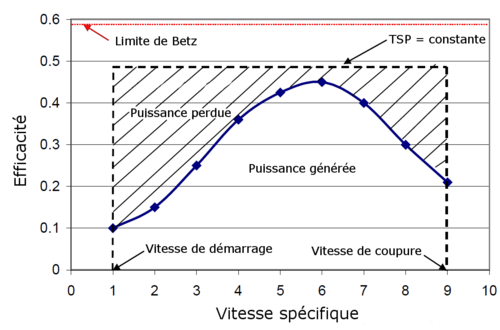
La vitesse spécifique
La vitesse spécifique ou le paramètre de rapidité noté λ (Lambda) en anglais Tip Speed Ratio (TSR) est le rapport entre la vitesse de l'extrémité des pales et la vitesse du vent. Les machines peuvent être classées en fonction de ce paramètre
- si λ est inférieur à 3, l’éolienne est dite lente
- si λ est supérieur à 3, l’éolienne est dite rapide
Par exemple, une éolienne bipales peut avoir un paramètre λ égal à 20.

 : Vitesse spécifique (sans unité)
: Vitesse spécifique (sans unité)
 : vitesse de l'extrémité des pales (en m/s)
: vitesse de l'extrémité des pales (en m/s)
 : vitesse du vent (en m/s)
: vitesse du vent (en m/s)
 : longueur des pales ou rayon de la turbine (en m)
: longueur des pales ou rayon de la turbine (en m)
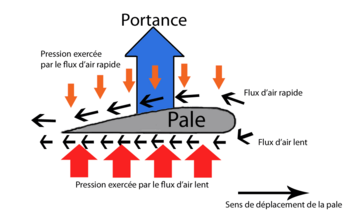
La portance
Comme pour l'aile d'un avion, une pale d'éolienne utilise l'effet de portance. Cet effet est du à l'écoulement de l'air autour du profil qui est plus rapide sur l'extrados (le dessus) que sur l'intrados (le dessous) de l'aile, ce qui entraine une dépression sur l'extrados. Le flux d'air circule plus rapidement sur l'extrados car la longueur à parcourir est plus importante que sous l'intrados, l'écoulement d'air devant rester constant à l'avant et à l'arrière de la pale, l'air s'écoule donc plus rapidement.
La portance est perpendiculaire à la direction du vent.

 : portance (en N)
: portance (en N)
 : masse volumique de l’air (1,225 kg/m3 à 15°C au niveau de la mer)
: masse volumique de l’air (1,225 kg/m3 à 15°C au niveau de la mer)
 : vitesse de déplacement : vitesse relative du vent par rapport à la pale (en m/s)
: vitesse de déplacement : vitesse relative du vent par rapport à la pale (en m/s)
 : surface de la pale (surface projetée, surface mouillée, maître couple) (en m2)
: surface de la pale (surface projetée, surface mouillée, maître couple) (en m2)
 : coefficient de portance, il est déterminé en soufflerie et est propre pour chaque profil de pale
: coefficient de portance, il est déterminé en soufflerie et est propre pour chaque profil de pale
On suppose que la surface S est égale à la surface réelle de la pale.

 : surface de la pale (en m2)
: surface de la pale (en m2)
 : corde de la pale (en m)
: corde de la pale (en m)
 : longueur de la pale (en m)
: longueur de la pale (en m)
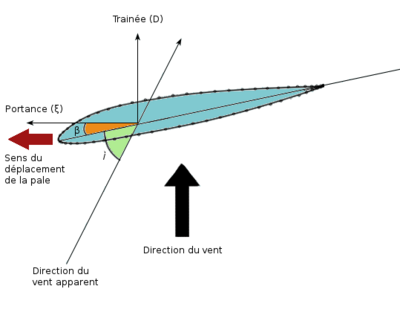
La traînée
En aérodynamique la traînée correspond à la résistance d'air, celle-ci augmente avec la surface exposée à la direction de l'écoulement de l'air. La traînée est une force qui agit sur la pale dans la même direction que le vent. Cette force tend à contrer le mouvement d’avancement de la pale et doit donc être la plus faible possible. La traînée est calculée de la façon suivante :

 : trainée (en N)
: trainée (en N)
 : masse volumique de l’air (1,225 kg/m3 à 15°C au niveau de la mer)
: masse volumique de l’air (1,225 kg/m3 à 15°C au niveau de la mer)
 : vitesse de déplacement (en m/s)
: vitesse de déplacement (en m/s)
 : surface de référence (surface projetée, surface mouillée, maître couple)
: surface de référence (surface projetée, surface mouillée, maître couple)
 : coefficient de traînée
: coefficient de traînée
Action aérodynamique
L’action aérodynamique totale ou résistance de l’air est la résultante de ces deux forces de trainée et de portance

 : force totale (en N)
: force totale (en N)
 : masse volumique de l’air (1,225 kg/m3 à 15°C au niveau de la mer)
: masse volumique de l’air (1,225 kg/m3 à 15°C au niveau de la mer)
 : vitesse de déplacement (en m/s)
: vitesse de déplacement (en m/s)
 : surface de référence (surface projetée, surface mouillée, maître couple)
: surface de référence (surface projetée, surface mouillée, maître couple)
 : coefficient aérodynamique total
: coefficient aérodynamique total
La finesse
La finesse du profil joue un rôle important. Elle doit être assez grande pour que la traînée n’absorbe pas une partie trop élevée du couple moteur.

 : finesse du profil (sans unité)
: finesse du profil (sans unité)
 : coefficient de portance (sans unité)
: coefficient de portance (sans unité)
 : coefficient de traînée (sans unité)
: coefficient de traînée (sans unité)
Pour maximiser le rendement d'une éolienne, il faut que la finesse soit maximale, autrement dit que la traînée soit minimale et la portance maximale. En général l'utilisation de 3 pales fines fonctionnant à une vitesse bien supérieure à celle du vent permet d'exploiter au maximum la portance tout en générant une traînée la plus faible possible.
La finesse d'un profil dépend de plusieurs paramètres :
- l'angle d'attaque de la pale (c'est à dire l'angle de la pale par rapport au vent apparent)
- la forme de la pale
- son facteur de forme
Angle d'attaque des pales
L’angle d’attaque est composé de la somme de l’angle d’incidence  et de l’angle de calage
et de l’angle de calage  des pales.
L’angle de calage est l’angle formé par la pale et le plan de rotation de la pale. L’angle d’incidence est l’angle formé par la pale et la direction apparente du vent. Comme la vitesse tangentielle de la pale augmente en s’éloignant du centre de rotation, la vitesse relative du vent
des pales.
L’angle de calage est l’angle formé par la pale et le plan de rotation de la pale. L’angle d’incidence est l’angle formé par la pale et la direction apparente du vent. Comme la vitesse tangentielle de la pale augmente en s’éloignant du centre de rotation, la vitesse relative du vent  et l’angle d’incidence changent. Pour conserver un angle d’attaque constant sur toute la longueur de la pale, il est possible de modifier l’angle de calage en vrillant la pale sur sa longueur.
et l’angle d’incidence changent. Pour conserver un angle d’attaque constant sur toute la longueur de la pale, il est possible de modifier l’angle de calage en vrillant la pale sur sa longueur.

 : angle d’attaque (en degrés)
: angle d’attaque (en degrés)
 : angle d’incidence (en degrés)
: angle d’incidence (en degrés)
 : angle de calage (en degrés)
: angle de calage (en degrés)
 : vitesse du vent (en m/s)
: vitesse du vent (en m/s)
 : vitesse tangentielle (en m/s)
: vitesse tangentielle (en m/s)
Le décrochage
Si on incline une pale ou une aile par rapport à la direction de l'écoulement de l'air, sa portance augmentera. Lorsque l'angle d'incidence - ou angle d'attaque - devient trop important il se produit un décrochage aérodynamique, cela signifie que l'écoulement de l'air sur l'extrados ne se fait plus de façon régulière, et l'air commence à tournoyer dans un tourbillon irrégulier en formant une turbulence. La portance résultant de la dépression au niveau de l'extrados de l'aile disparaît.
Le phénomène de décrochage aérodynamique est utilisé par les ingénieurs de l'industrie éolienne lors de la conception des pales du rotor (système de régulation et de protection).
Diminution de vitesse en aval du rotor
Le modèle le plus courant de calcul de la diminution de vitesse dans le sillage est celui développé par WASP/Park2, logiciel utilisé en standard par l’industrie éolienne. Ce modèle s’appuie sur le développement linéaire d’un Sillage rectangulaire.
![Equation $$
v = U \bigg[ 1-\sqrt{({1-CT})}(\frac{D}{D+2kX})^2\bigg]
$$](/lib/exe/fetch.php?media=wiki:latex:/imgd36281fe09b7113af6a2035aa0ee41a0.png)
 : vitesse du vent dans le sillage, en aval du rotor tournant (en m/s)
: vitesse du vent dans le sillage, en aval du rotor tournant (en m/s)
 : vitesse du vent non perturbée en amont (en m/s)
: vitesse du vent non perturbée en amont (en m/s)
 : coefficient de traînée de l’éolienne (sans dimension)
: coefficient de traînée de l’éolienne (sans dimension)
 : diamètre du rotor (en m)
: diamètre du rotor (en m)
 : distance du rotor au point de calcul (en m)
: distance du rotor au point de calcul (en m)
 : est une constante de décroissance du sillage
: est une constante de décroissance du sillage

 : constante (A=0,5)
: constante (A=0,5)
 : hauteur du moyeu (centre du rotor)
: hauteur du moyeu (centre du rotor)
 : longueur de rugosité
: longueur de rugosité
Électricité
La chute de tension
 d'un câble électrique
d'un câble électrique
 avec
avec 
 : longueur du câble (en m)
: longueur du câble (en m)
 : section de câble (en m2)
: section de câble (en m2)
 : résistivité du matériau utilisé (cuivre :
: résistivité du matériau utilisé (cuivre :  Aluminium
Aluminium  )
)
 : intensité nominale (en ampère)
: intensité nominale (en ampère)
 : nombre de conducteurs (mono ou triphasé)
: nombre de conducteurs (mono ou triphasé)
Puissance d'une turbine
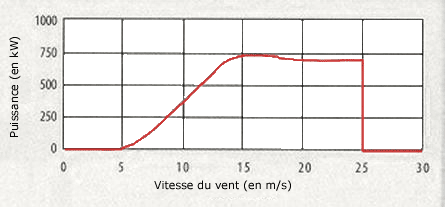
La courbe de puissance d'une éolienne
La courbe de puissance est un graphe qui représente la puissance de sortie d'une éolienne à différentes vitesses de vent.
Elle est élaborée à partir de mesures effectuées sur site en fixant un anémomètre sur un mât situé à proximité de l'éolienne et non directement sur l'éolienne même ou trop près de celle-ci car elle risque alors de provoquer des turbulences qui nuiront à la fiabilité des mesures.
La courbe de puissance est en réalité constituée d'une multitude de points espacés de part et d'autre de la ligne rouge, plutôt qu'une courbe bien définie comme celle du graphe ci-contre. En effet, il y aura toujours des fluctuations de la vitesse du vent qui rendront impossible une mesure de façon précise du flux d'air passant à travers le rotor de l'éolienne. Dans la pratique, on prendra donc la moyenne des différentes mesures pour chaque vitesse de vent afin de tracer le graphe. Une erreur de mesure de 3% de la vitesse du vent engendrera une erreur de 9% du contenu énergétique du vent. Par conséquent, une marge d'erreur de +/- 10% est possible, même dans les courbes de puissance certifiées.
On peut distinguer 4 parties sur cette courbe :
- de 0 à la vitesse de démarrage (ici 5 m/s) : la puissance de sortie est nulle, le vent n'est pas suffisamment important pour entraîner la rotation du rotor
- de la vitesse de démarrage à le vitesse nominale (ici 15 m/s) : la puissance de sortie augmente jusqu'à atteindre la puissance nominale (ici 750 kW)
- de la vitesse nominale à la vitesse de coupure (ici 25 m/s) : la puissance de sortie est maintenue à la puissance nominale presque constante grâce au dispositif de régulation.
- après la vitesse de coupure : l’éolienne est mise à l’arrêt pour protection, la puissance de sortie est nulle
Utilisation
Une courbe de puissance n'indique pas la puissance effective d'une éolienne à une certaine vitesse moyenne du vent. Il est très important de savoir comment cette moyenne a été calculée, c'est à dire si le vent est très variable, ou s'il souffle à une vitesse relativement constante.
Par exemple un site présentant une vitesse de vent moyenne annuelle de 5 m/s, si l'on suppose que cette année fasse 8000 heures :
- si le vent souffle pendant 8000 heures à 5 m/s nous obtiendront 2000 kWh à la fin de l'année (pour une puissance constante de 250 Watts)
- si le vent ne souffle pas pendant 4000 heures (production nulle) et souffle pendant 4000 heures restantes à 10 m/s nous obtiendront une production de 8000 kWh (pour une puissance constante de 2 kW).
Dans ces deux cas la moyenne du vent annuelle est identique, mais dans la production, dans le deuxième cas, est 4 fois plus importante. C'est pour cela qu'une mesure, pendant une durée d'au minimum une année, de la vitesse du Le vent sur le site est très importante afin de tenir compte des variations saisonnières qui peuvent avoir une influence très importante sur la production de l'éolienne.
De plus, la plupart de l'énergie éolienne est captable à des vitesses de vent deux fois supérieures à la vitesse de vent la plus fréquente sur le site en question (voir densité de puissance). Il faudra aussi prendre en compte le fait que l'éolienne ne se trouvera peut-être pas sur un site avec une pression d'air et une température standard. Dans ce cas, il faudra corriger la courbe en fonction des variations de la densité de l'air.
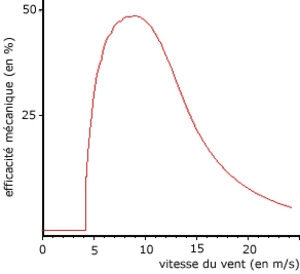
Efficacité mécanique
Sur ce graphe, l'efficacité mécanique de l'éolienne est la plus élevée (45 %) pour une vitesse de vent d'environ 9 m/s. Cette valeur a été choisie délibérément par les ingénieurs lors de la conception de l'éolienne. A des vitesses de vent faibles, l'efficacité a moins d'importance car il y a peu d'énergie à récupérer. A des vitesses de vent élevées, l'éolienne est mise en drapeau afin de ne pas la détériorer, l'énergie n'est donc pas récupérable. Il est donc plus intéressant d'avoir une bonne efficacité à des vitesses de vent où la plus grande partie de l'énergie est récupérable.
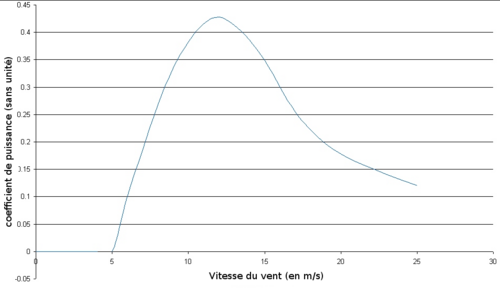
Le coefficient de puissance
Le coefficient de puissance ou coefficient de performance indique l'efficacité avec laquelle l'éolienne convertit l'énergie mécanique du vent en électricité. Ce coefficient diffère suivant les turbines. On commence par prendre la courbe de puissance et on la divise par la surface balayée par le rotor afin d'obtenir la puissance de sortie par mètre carré de surface balayée. On divise ensuite ce résultat par la puissance du vent par mètre carré pour chaque vitesse de vent.
Le graphe ci-contre représente la courbe du coefficient de puissance pour une éolienne, bien que l'efficacité moyenne d'une telle éolienne soit normalement supérieure à 20 %, celle-ci varie considérablement en fonction de la vitesse du vent.
Le coefficient de puissance tient compte de la limite de Betz, c'est pour cela qu'il sera toujours inférieur à cette limite, il est de l'ordre de 35 % pour une éolienne à axe horizontal il ne dépasse pas 10 % pour une éolienne axe vertical2).
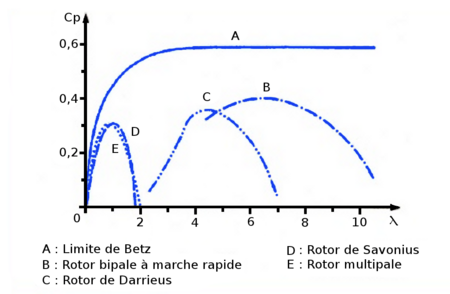
Coefficient de puissance de différents rotors
Sur ce graphiques différents coefficients de puissance suivant différents rotors.
Calcul du coefficient de puissance
Ce calcul est une valeur approchée de manière empirique pour une éolienne utilisant une génératrice de type MADA.
![Equation $$Cp = [0.5 - 0.00167.(\beta -2)].sin\left(\dfrac{\pi(\lambda + 0.1)}{18.5 - 0.3(\beta - 2)}\right) - 0,00184(\lambda - 3)(\beta - 2) $$](/lib/exe/fetch.php?media=wiki:latex:/img9d447bed316a86069643cbe3dd7ad629.png)
 : Vitesse spécifique (sans unité)
: Vitesse spécifique (sans unité)
 : Angle de calage des pales (en degrés)
: Angle de calage des pales (en degrés)
Couple mécanique produit par l'éolienne

 : couple mécanique produit par l'éolienne (en N·m)
: couple mécanique produit par l'éolienne (en N·m)
 : puissance mécanique (en W)
: puissance mécanique (en W)
 : fréquence de rotation du rotor (en rad/s)
: fréquence de rotation du rotor (en rad/s)
Le couple moteur est la force de rotation qui fait tourner le rotor. Ce couple est obtenu par une sommation des composantes de portance et de traînée et est fonction du nombre de pales du rotor :
![Equation $$\Gamma = \int_{D}^{L}\, d\Gamma = \eta \cdot \int\limits_{D}^{L}\left [ \xi \cdot \sin \alpha - D \cdot \cos \alpha \right ]$$](/lib/exe/fetch.php?media=wiki:latex:/imgafdd66b259398fbbe2f19a833af17b05.png)
 : couple moteur (en N·m)
: couple moteur (en N·m)
 : nombre de pales (sans unité)
: nombre de pales (sans unité)
 : angle d'attaque des pales (en degrés)
: angle d'attaque des pales (en degrés)
 : Portance (en N)
: Portance (en N)
 : trainée (en N)
: trainée (en N)
 : longueur des pales (en m)
: longueur des pales (en m)
En supposant l'angle  constant sur toute la longueur de la pale il est possible de simplifier cette équation en considérant une vitesse relative constante sur toute la longueur de la pale. On trouve que le couple moteur peut s’exprimer sous la forme suivante :
constant sur toute la longueur de la pale il est possible de simplifier cette équation en considérant une vitesse relative constante sur toute la longueur de la pale. On trouve que le couple moteur peut s’exprimer sous la forme suivante :
![Equation $$\Gamma = \eta \cdot L \cdot \left [ \xi \cdot \sin \alpha - D \cdot \sin \alpha \right ] $$](/lib/exe/fetch.php?media=wiki:latex:/img18c05e5299a9b7f9f854de65b59676a0.png)
![Equation $$ = \eta \cdot L^2 \cdot \frac{\rho \cdot c}{2} \cdot \left ( v^2 + \frac{1}{\sqrt{3}} \cdot U^2 \cdot \left [ C_z \cdot \sin \alpha \cdot C_x \cdot \cos \alpha \right ] \right ) $$](/lib/exe/fetch.php?media=wiki:latex:/img5a4d9d139bcecc3b1ff043c47f9424db.png)
 : couple moteur (en N·m)
: couple moteur (en N·m)
 : nombre de pales (sans unité)
: nombre de pales (sans unité)
 : angle d'attaque des pales (en degrés)
: angle d'attaque des pales (en degrés)
 : Portance (en N)
: Portance (en N)
 : trainée (en N)
: trainée (en N)
 : longueur des pales (en m)
: longueur des pales (en m)
Puissance mécanique à l’entrée de la génératrice

 : Puissance mécanique à l’entrée de la génératrice (en W)
: Puissance mécanique à l’entrée de la génératrice (en W)
 : masse volumique de l'air (air atmosphérique sec, environ : 1,23 kg/m3 à 15 °C et à pression atmosphérique 1,0132 bar)
: masse volumique de l'air (air atmosphérique sec, environ : 1,23 kg/m3 à 15 °C et à pression atmosphérique 1,0132 bar)
 : longueur des pales ou rayon de la turbine (en m)
: longueur des pales ou rayon de la turbine (en m)
 : vitesse du vent (en m/s)
: vitesse du vent (en m/s)
 : Coefficient de performance (sans unité)
: Coefficient de performance (sans unité)
 : Vitesse spécifique (sans unité)
: Vitesse spécifique (sans unité)
 : Angle de calage des pales (en degrés)
: Angle de calage des pales (en degrés)
Pertes et rendements
Les différentes pertes réduisant l'efficacité aérodynamique du rotor rentrant en jeu lors du fonctionnement d'une éolienne sont :
- pertes dues au nombre de pales
- pertes dues aux turbulences
- les pertes en bout de pales
- pertes liées au profil aérodynamique des pales (aile)
Pertes de profil
Ces pertes sont liées à la finesse du profil.

 : rendement du profil (sans unité)
: rendement du profil (sans unité)
 : finesse du profil (sans unité)
: finesse du profil (sans unité)
 : Vitesse spécifique (sans unité)
: Vitesse spécifique (sans unité)
Pertes en bout de pale
A la pointe des pales, une circulation d'air (appelé fuites ou tourbillon marginal) apparaît du bas de la pale vers le haut de la pale créant une turbulence en bout de pale. Ce flux d'air interfère avec le vent incident arrivant sur la pale générant ainsi une perte, noté  . Plus la portance près du bout de l'aile sera importante et plus il y a de fuites. Plus la pale ou l'aile est courte plus il y a de fuites. Une winglet (ailette sensiblement verticale) située au bout des pales permet de réduire la traînée induite.
. Plus la portance près du bout de l'aile sera importante et plus il y a de fuites. Plus la pale ou l'aile est courte plus il y a de fuites. Une winglet (ailette sensiblement verticale) située au bout des pales permet de réduire la traînée induite.
Production d'énergie annuelle
Variation de la production d'énergie par rapport à la vitesse du vent
La production d'énergie varie presque avec le cube de la vitesse du vent.
La densité de l’air entre également en jeu : une éolienne produit 3 % de plus d’électricité si, pour une même vitesse de vent, l’air est 10 degrés inférieur. Les précipitations n’ont, quant à elles, aucune influence.
Le facteur de charge
Le facteur de charge d'une éolienne sur un site correspond à sa production annuelle divisée par la production théorique maximale de cette éolienne si elle fonctionnait à sa puissance nominale (maximale) pendant l'ensemble des 8 766 heures (365,25 x 24) que compte une année. Le facteur de charge correspond au ratio entre la quantité réelle d'énergie produite sur une année et la production théorique maximale d'une éolienne fonctionnant à pleine puissance à plein temps.
Par exemple, pour une éolienne de 500 kW produisant 1,2 millions de kWh en un an on aura un facteur de charge égal à 1 200 000.103/(8 766 x 500.103) = 0,274 soit 27,4%. En théorie, un facteur de charge est compris entre 0% et 100%, dans la pratique il se trouvera plutôt compris entre 25% et 30%.
Les éoliennes ne sont pas principalement conçues pour un facteur de charge optimal, mais pour générer autant d'électricité que possible à une certaine vitesse de vent.
Bien qu'un facteur de charge élevé soit en général à préférer, ce n'est pas obligatoirement un avantage d'un point de vue économique. Sur un site très venté il sera peut être plus judicieux économiquement d'utiliser une éolienne avec un plus petit rotor (donc une capacité plus faible qu'avec un rotor plus grand) mais qui sera moins chère.