Theoretical study of a wind turbine
Wind energy
Kinetic energy
The wind is air in motion, and as any body in movement we can associate it a kinetic energy, which is a function of the mass and velocity of the air volume. If we consider that the air density (mass per unit of volume) is constant, we can say that the energy supplied by the wind is a function of speed:

 : mass of air volume (in kg)
: mass of air volume (in kg)
 : instantaneous wind speed (in m/s)
: instantaneous wind speed (in m/s)
 : kinetic energy (in joules)
: kinetic energy (in joules)
The air mass
At normal atmospheric pressure and at 15 degrees Celsius temperature air weighs about 1.225 kilograms per cubic meter. However, the density decreases slightly when the humidity increases. Similarly, the cold air is more dense than warm air, as the air density is lower at high altitudes (in the mountains) due to the lower air pressure that prevails.

 : mass of air volume (in kg)
: mass of air volume (in kg)
 : air volume occupied (in m3)
: air volume occupied (in m3)
 : density (in kg/m3)
: density (in kg/m3)
In the case of wind power, the air volume occupied depends on the area swept by the rotor of the wind turbine. The power of the wind through the rotor corresponds to the amount of kinetic energy the rotor through every second.
Theoretically harvest-able energy
Considering a collection device of this energy of surface S and assuming that the wind velocity is the same at each point of the surface, the volume of air passing through this surface in one second is equal to VS.

 : recoverable power (Watt)
: recoverable power (Watt)
 : mass flow of the volume of air passing through the surface S in 1 second (kg/s)
: mass flow of the volume of air passing through the surface S in 1 second (kg/s)
 : air density (kg/m3)
: air density (kg/m3)
 : air velocity through the device (m/s)
: air velocity through the device (m/s)
 : surface of the collecting device (m2)
: surface of the collecting device (m2)
 : air volume flow (m3/s)
: air volume flow (m3/s)
Which is equivalent to the following formula.
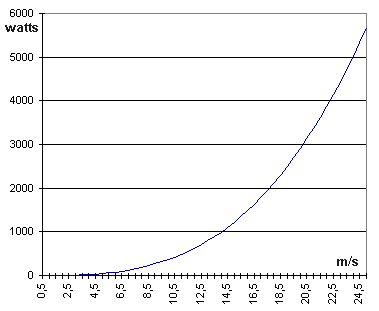
Recoverable power

 : air density (atmospheric dry air, about: 1,23 kg/m3 at 15 °C and at atmospheric pressure 1,0132 bar)
: air density (atmospheric dry air, about: 1,23 kg/m3 at 15 °C and at atmospheric pressure 1,0132 bar)
 : rotor surface (in m2)
: rotor surface (in m2)
 : Wind speed (in m/s)
: Wind speed (in m/s)
This power is a theoretical power, of course it is not possible that the totality of this power would be harvested by a wind turbine (this would stop the wind).
Wind turbines are diverting wind
In practice, a wind turbine is used to recover energy from the wind, in return the wind turbine deflects the wind before it reaches the rotor swept area. A wind turbine will never be able to recover the total energy supplied by the wind (see Betz 'law). When the kinetic energy of wind is converted into mechanical energy by the rotor, the wind is braked by the rotor, the wind speed at the upstream rotor is always greater than downstream. But, the air mass flow through the area swept by the rotor is the same as that the air mass going out of the rotor. This results in an enlargement of the air stream (flow tube) to the rear of the rotor. The wind deceleration is progressive, until the velocity of the air at the rear of the rotor becomes almost constant.
Variation of the air density
Density ( ) varies with different parameters:
) varies with different parameters:
- The altitude (air pressure): the higher the altitude is, lower density of the air is. A single wind turbine will produce more at seaside than in mountain with the same wind speed
- The temperature : the higher the temperature is, lower the density of the air is. A wind turbine will produce more when with low ambient temperature
- Relative humidity of the air: if the air is more humid, the density will be higher but the influence of the relative humidity of the air density is relatively low
Betz limit / Betz Formula
The recoverable power is lower, because the air must maintain a residual kinetic energy to keep an air flow. German Albert Betz showed in 1919 that the maximum recoverable power is:

with  ,when
,when 
 : fluid density (atmospheric dry air, about: 1,23 kg/m3 at 15 °C and at atmospheric pressure 1,0132 bar)
: fluid density (atmospheric dry air, about: 1,23 kg/m3 at 15 °C and at atmospheric pressure 1,0132 bar)
 : wind sensor surface (in m2)
: wind sensor surface (in m2)
 : incident fluid speed (uphill) (in m/s)
: incident fluid speed (uphill) (in m/s)
The maximum theoretical yield of a wind turbine is set as  , approximately 59.3%. This figure does not take into account energy losses incurred during the conversion of mechanical wind energy into electrical energy.
, approximately 59.3%. This figure does not take into account energy losses incurred during the conversion of mechanical wind energy into electrical energy.
In the case of a helix of diameter D, the Betz limit is equal to:


The power delivered by a wind turbine is proportional to:
- the rotor dimensions to the square
- the wind speed to the cube
Yields
The energy supplied by the aerogenerator is converted from one form to another, this limit is affected by all yiels related to different transformations.
- Propeller:

- The multiplier or gearbox:

- The alternator or the continue current generator:

- The transformer:

- The rectifier:

- The batteries:

- Line losses:

Yields of every element varies with the operating conditions related to the rotational speed of the propeller, which outside of rated speed, further reduces the overall performance of the device, it is difficult to exceed 70% of the Betz limit.
The wind potential
The Weibull distribution
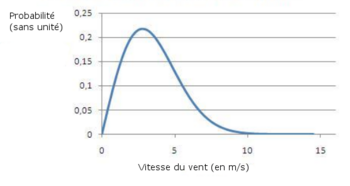
We normally describes the variations of the wind on a given site using a Weibull distribution as the one you see in the image below. This is the general model that describes the variations of the wind speed. This model helps to optimize the design of wind turbines to minimize electricity generation costs .
The coefficient reflects the Weibull distribution of wind speeds and is determined by the Weibull distribution curve.
Construction
Measuring the average wind speed every 10 minutes by thanks to an anemometer. The values obtained are then divided into different wind speeds. We can then express the energy potential of a site based on the frequency of different wind speed classes.
Weibull density probability function

The probability density function of Weibull intended to reflect the likelihood of an event to occurre between two points. The area under the curve between two wind speeds greater than zero is equal to the probability that the wind blow somewhere between these two speeds. On the folowing power curve, we can determine the constants of the Weibull parameters:
 is the Weibull shape factor. It gives the shape of the distribution and takes a value between 1 and 3. The lower the value is the more variable the wind speed is, while a high value of k indicates a constant wind speed.
is the Weibull shape factor. It gives the shape of the distribution and takes a value between 1 and 3. The lower the value is the more variable the wind speed is, while a high value of k indicates a constant wind speed.
 is the Weibull scale factor expressed in m/s. It can express the chronology of a characteristic velocity.
is the Weibull scale factor expressed in m/s. It can express the chronology of a characteristic velocity.  is proportional to the mean wind speed.
is proportional to the mean wind speed.
In the case of the folowing curve:
- Shape factor: k = 1.751311
- Scale factor: c = 5.986052.
The area under the curve is defined by:

In this example, the probability that the wind blows between 3 m/s and 4 m/s is: F (4) - F (3) = 0.38958 - 0.25788 or 13.17%
The Rayleigh distribution
In the case where the value of the shape parameter (k) is exactly 2, the distribution is called Rayleigh distribution. The wind turbine manufacturers often provide performance calculations using the Rayleigh distribution.
The wind average power
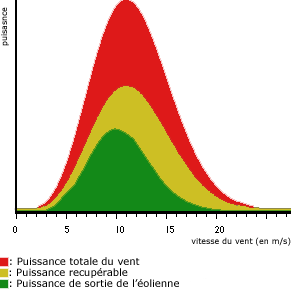
The average wind power is determined by the Weibull distribution, determine the average wind speed is not enough to calculate the average power. We have to take into account the probability of occurrence of each wind speed and the corresponding power, because the power is proportional to the cube of the wind speed. Strong winds containing more energy will have more influence on the average power, although they have a low probability.
The wind power
Multiplying the power of each wind speed by the probability of the occurrence of this speed according to Weibull distribution, we can calculate the distribution of wind power at different wind speeds, this distribution is called the power density.
Wind speed variation according to the altitude
Action of the wind on the blades
Rotor angular speed
Angular speed  , also called angular frequency or pulsation, is a measure of the rotation speed. Namely, angle in seconds
, also called angular frequency or pulsation, is a measure of the rotation speed. Namely, angle in seconds

 : angular speed (in rad/s)
: angular speed (in rad/s)
 : rotor rotation frequency (in s-1)
: rotor rotation frequency (in s-1)
Tangential speed
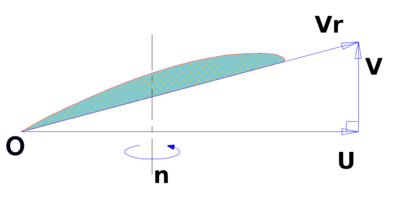
Considering an immobile helix whose axis of rotation is parallel to the wind direction, for each blade we can plot the resultant perpendicular to the profile applied to the center of the aerodynamic thrust.
Is obtained:
 and
and  parallel in the same direction that tend to move the propeller in a translational motion in the direction of the wind
parallel in the same direction that tend to move the propeller in a translational motion in the direction of the wind and
and  parallel and opposite directions perpendicular to the wind direction
parallel and opposite directions perpendicular to the wind direction
These two forces create a torque tending to rotate the helix in a plane perpendicular to the wind direction.

 : wind speed due to the displacement of the blade or tangential speed (in m/s)
: wind speed due to the displacement of the blade or tangential speed (in m/s)
 : distance from the considered point to the axis of rotation (in m)
: distance from the considered point to the axis of rotation (in m)
 : rotor angular velocity (in rad/s)
: rotor angular velocity (in rad/s)
 : rotational frequency of the rotor (in rpm)
: rotational frequency of the rotor (in rpm)
Relative speed
The wind speed saw by the blade is in fact a composition between the real wind and the wind created by the blade motion (which varies along the length of the blade in proportionally to the radius), the resulting wind is called apparent wind or relative wind, the speed of this resulting wind from the blade is greater than the velocity of the blade itself.
From the Pythagorean theorem, the square relative velocity is given by the sum of squares of the wind speed and the tangential velocity of the blade.

 : relative speed of the blade (in m/s)
: relative speed of the blade (in m/s)
 : wind speed (in m/s)
: wind speed (in m/s)
 : tangential velocity of the point in question (in m/s)
: tangential velocity of the point in question (in m/s)