Table des matières
Démonstration de la limite de Betz
Hypothèses
- L'étude est réalisée dans un référentiel
 lié au sol et supposé galiléen
lié au sol et supposé galiléen - L'air est considéré comme un fluide parfait, homogène et incompressible de masse volumique

- On suppose que le mouvement de l'air est stationnaire et à symétrie de révolution autour de l'axe de rotation de l'hélice
Puissance cinétique
Calculons maintenant la masse d'air déplacée en amont du rotor par unité de temps :

 étant la masse volumique de l'air exprimée en kg/m3
étant la masse volumique de l'air exprimée en kg/m3
La puissance cinétique de cette masse d'air avant qu'elle ne frappe la turbine est donnée par :



Nous procédons de la même façon pour calculer  , la puissance cinétique en aval du rotor
, la puissance cinétique en aval du rotor

Variation d’énergie cinétique
La variation d’énergie cinétique par unité de temps de la masse d'air qui passe au travers le rotor est donc égale à (en remplaçant la densité de l’air par sa valeur moyenne) :




Puissance absorbée par le rotor
Calculons maintenant l'énergie absorbée par le rotor. La variation de la quantité de mouvement de la veine de vent entre l'amont et l'aval du rotor s'exprime par la relation vectorielle :

Avec

La variation de quantité de mouvement par unité de temps de la veine de vent entre l'amont et l'aval du rotor vaut donc :

Nous pouvons en déduire que la puissance perdue par la veine de vent et donc absorbée par le rotor est égale à :

en admettant que les vitesses du vent en amont et en aval du rotor ont la même direction.
Or nous savons que cette puissance est égale à l’opposé de la variation d’énergie cinétique par unité de temps soit :

En remplaçant  et
et  par leurs expressions trouvées précédemment, nous avons l'égalité suivante :
par leurs expressions trouvées précédemment, nous avons l'égalité suivante :

en développant l'identité remarquable du type a2-b2 nous avons

Nous pouvons en déduire l'expression de 

Puissance maximale
Déterminons maintenant  pour que la puissance
pour que la puissance  soit maximale
soit maximale

En remplaçant  par son expression calculée précédemment nous avons
par son expression calculée précédemment nous avons


La puissance  est maximale pour une vitesse
est maximale pour une vitesse  telle que sa dérivée première s'annule et que sa dérivée seconde est négative.
telle que sa dérivée première s'annule et que sa dérivée seconde est négative.

soit

C'est-à-dire

On résout cette équation du second degré et d’inconnue 

Nous avons 2 solutions possibles

cette solution est impossible
ou

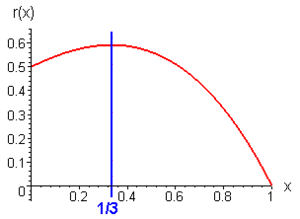
 est donc maximale pour
est donc maximale pour  égal à
égal à 
On vérifiera que la dérivée seconde est bien alors négative.
Calcul de la puissance maximale
Nous savons que

Donc d’après la valeur maximale de 

En reportant  et
et  dans l'expression de
dans l'expression de  on obtient :
on obtient :

D’où

Calcul du coefficient d'énergie maximal
Nous savons que la puissance récupérable du vent s'exprime par

Nous pouvons donc écrire  sous cette forme, soit
sous cette forme, soit

Par identification nous en déduisons la valeur de  , nous retrouvons la limite de Betz, nous venons donc de la démontrer.
, nous retrouvons la limite de Betz, nous venons donc de la démontrer.